Skip to main content

加密算法笔记

加密学笔记

摘要算法#

维基没有对应词条，有散列函数，两者本质一样。

  • 定义：又称散列算法、哈希函数，是一种从任何一种数据中创建小的数字“指纹”的方法。
  • 常见的摘要算法有 MD5、SHA 等。

对称加密#

  • 定义：这类算法在加密和解密时使用相同的密钥，或是使用两个可以简单地相互推算的密钥。
  • 常见的对称加密算法有DES、3DES、AES、Blowfish、IDEA、RC5、RC6。
  • 对称加密的速度比公钥加密快很多，在很多场合都需要对称加密。

非对称加密#

  • 定义：也称为公开密钥加密。
  1. 它需要两个密钥，一个是公开密钥，另一个是私有密钥；一个用作加密，另一个则用作解密。两个密钥不同。
  2. 使用其中一个密钥把明文加密后所得的密文，只能用相对应的另一个密钥才能解密得到原本的明文；甚至连最初用来加密的密钥也不能用作解密。
  3. 虽然两个密钥在数学上相关，但如果知道了其中一个，并不能凭此计算出另外一个；因此其中一个可以公开，称为公钥，任意向外发布；不公开的密钥为私钥，必须由用户自行严格秘密保管。
  • 关键核心是找到一种算法，正向运算很方便，逆向运算很复杂。这种算法又称暗门算法

RSA加密算法#

  • 正向：素数乘法；反向：因数分解
  • 算法介绍参考维基

椭圆曲线#

曲线函数：$y^2 = x^3 + ax + b$

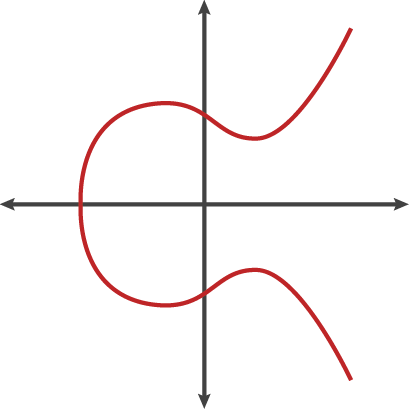
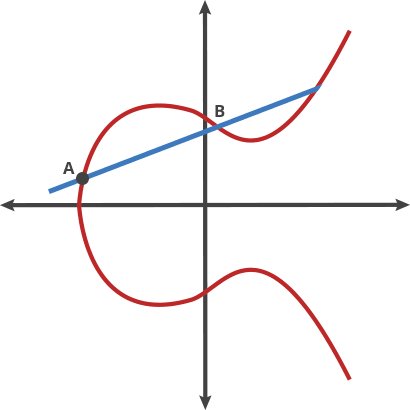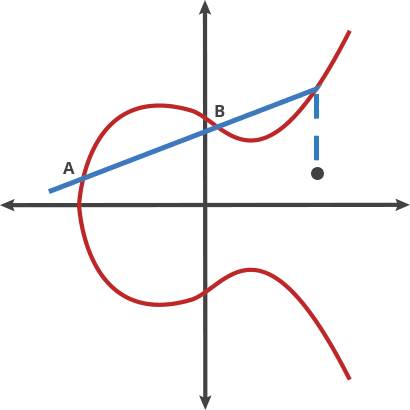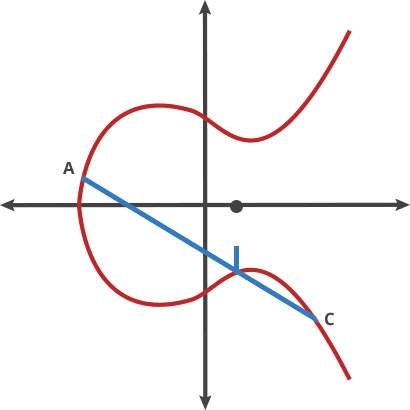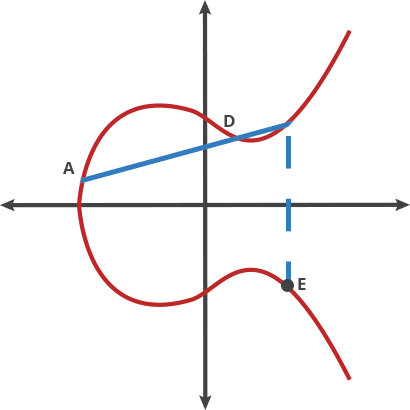
  • 定义算法：定义曲线上两点的加法表示，经过两点的直线与椭圆曲线相交的第三个点关于x轴的对称点。注意这个点还是在椭圆曲线上，因为椭圆曲线本身关于x轴对称。若相加的两点为同一个点，则作椭圆曲线在该点的切线。

$$2A = A + A = B$$ $$3A = A + B = C$$ $$4A = A + C = D$$ $$...$$

  • 正向：$nA = B$；逆向：由$B$求$A$
  • 密钥：$n$；公钥：$A, B$
  • 可以通过选择一个作为最大值的素数、曲线方程和曲线上的公共点来定义一个椭圆曲线密码系统。